In order to evaluate the energetic quality of a compressor (as with all energy machines) an efficiency is calculated. With piston compressors also a volumetric efficiency is being used, which is defined as the useable part of the piston displacement for gas discharge.
Energetic efficiency
The isothermal efficiency compares the power requirement for an isothermal compression with the actually required power input.
The isothermal power is the product of mass flow and the mass specific work required at ideal isothermal conditions. The mass flow of the compressor can be obtained by measuring the volume flow and the corresponding thermodynamic conditions, e.g. at suction side. With additional measurement of the discharge pressure, the isothermal work can be calculated.
The power required is the power input at the clutch, which is obtained by measuring the torque and the revolutions per minute.
A part of the power input is used up as the mechanical power loss (friction in the drive mechanism and at the sealing elements), as well as the work input of auxiliary aggregates such as lubricators, cooling pumps etc.).
The remaining internal work, which is transmitted by the piston onto the gas, is larger than the isothermal power, see Table 5.8.
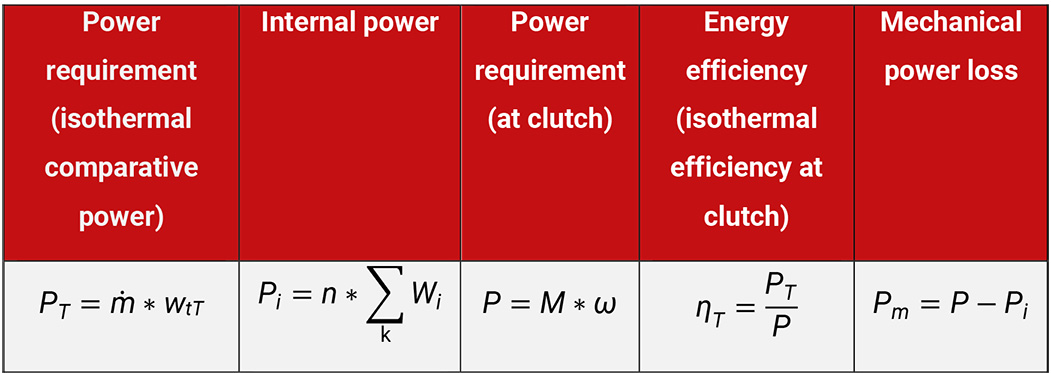
Table 5.8: Calculation of parameters to describe the energy efficiency
After the experimental evaluation (indicating) of the cylinder pressure, which varies with time and crank angle, or by simulating the thermodynamic processes by a calculation which comes close to the real conditions, the internal work can be derived by the areas of the p,V-diagrams of all working chambers .
The following diagram shows the principle relationship of the isothermal efficiency and the pressure ratio for air compressors with different number of stages, see Figure 5.6.
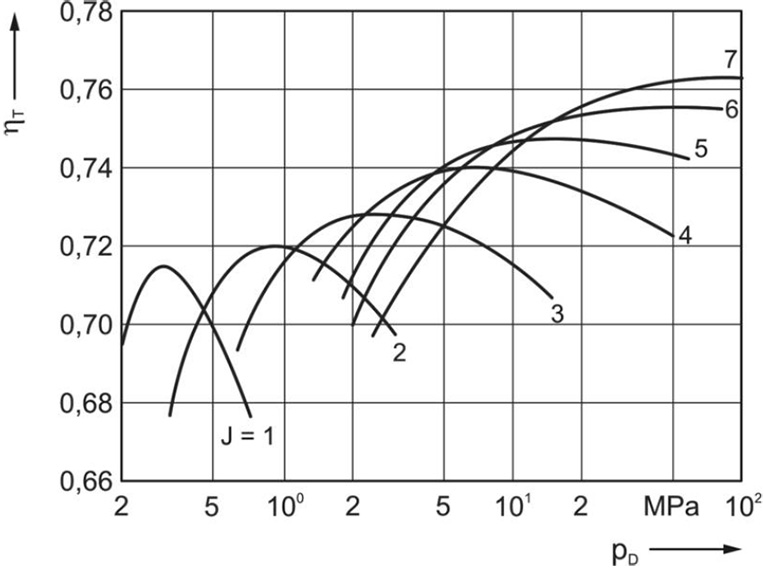
Figure 5.6: Relationship between the isothermal efficiency and the pressure ratio [0]
For each stage, there is an optimal pressure ratio from an energy efficiency perspective. With smaller pressure ratios the throttling losses become more important. With larger pressure ratios the additional work due to deviations from the isothermal compression rises. The maximum achievable efficiency rises with the number of stages, as the approximation to the isothermal process increases.
Volumetric efficiency
In the ideal case, the complete piston displacement at the end of the suction stroke is filled with gas at inlet condition. It would contain the complete displacement mass. The actual discharged mass after a compression cycle is always smaller than the ideal piston displacement mass.
The ratio of the actual delivered mass to the ideal mass per compression cycle or the respective mass flows is called the volumetric efficiency. This parameter does not give a direct indication of the energy efficiency of the compressor, although it comprises losses that also effect the energy efficiency.
If the piston displacement and the volumetric efficiency of a compressor is known, the volume flow (flow at suction condition) follows, see Table 5.9.
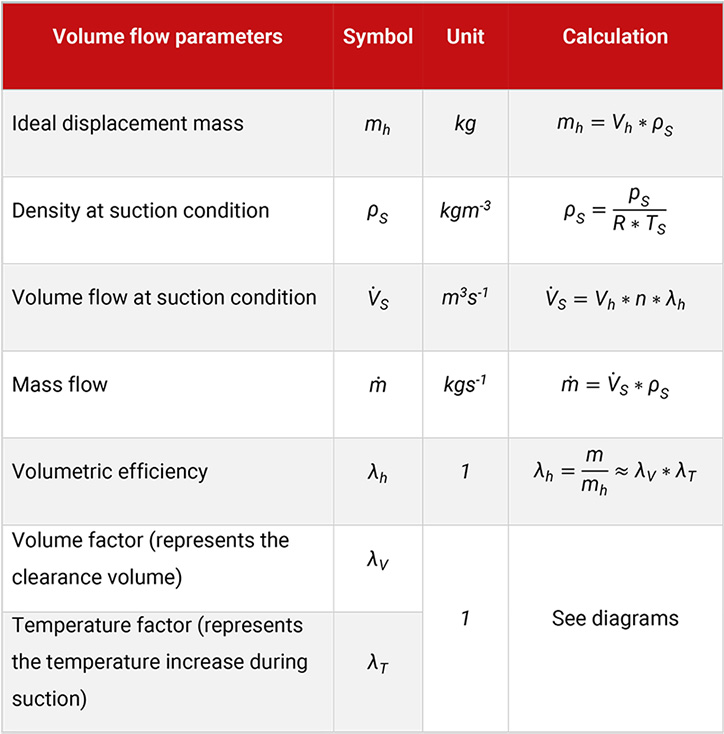
Table 5.9: Volume flow parameters
Figure 5.7 show the volume factor and the temperature factor depending on pressure ratio π, the clearance volume ratio ε0, and the polytropic exponent π.
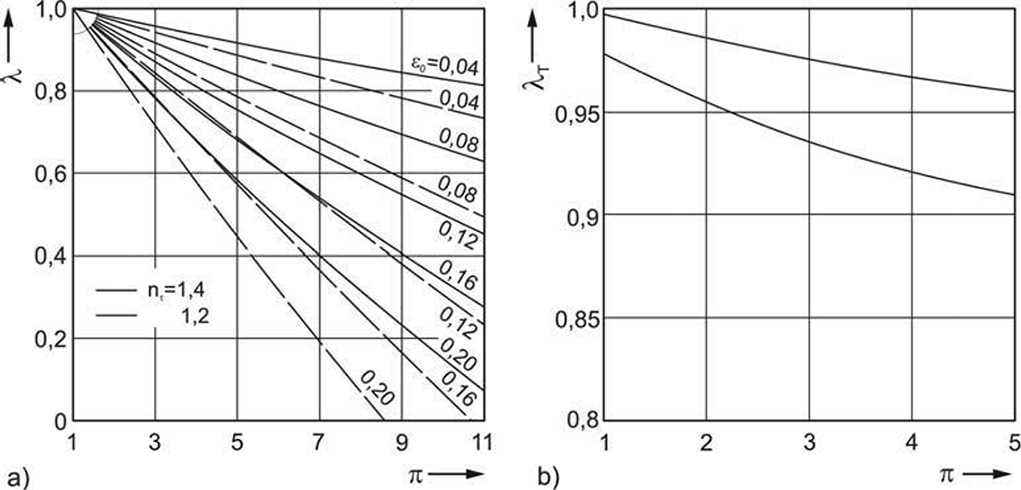
Figure 5.7: Volume factor (left) and Temperature factor (right) [0]

